11263. Четное дерево

Задано дерево – простой связный граф без циклов.

Найдите максимальное количество ребер, которое можно удалить из дерева так, чтобы получился лес, в котором каждая компонента связности содержала четное число вершин.

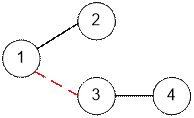
Например, в дереве с 4 вершинами можно удалить не более 1 ребра, чтобы получился четный лес.

Вход. Первая строка содержит два целых числа n (2 ≤ n ≤ 100, n четное) – количество вершин, и m – количество ребер. Каждая из следующих m строк содержит по два целых числа – номера вершин, соединенные ребром. Корнем дерева является вершина 1.

Выход. Выведите наибольшее возможное количество удаленных ребер.

Пример входа	Пример выхода
10 9 2 1 3 1 4 3 5 2 6 1 7 2 8 6 9 8 10 8	2

РЕШЕНИЕ

графы - поиск в глубину

Анализ алгоритма

В задаче следует совершить декомпозицию дерева на компоненты связности с четным числом вершин. При этом следует максимизировать количество этих компонент.

Запустим поиск в глубину из вершины 1, которая является корнем дерева. Для каждой вершины v определим количество вершин в поддереве с корнем v. Если это количество четное, то удалим ребро, соединяющее v с его предком при поиске в глубину.

Для корня (вершины 1) размер всего дерева четный. Однако ребра, соединяющего вершину 1 с ее предком, не существует. Поэтому из результата, полученного по выше приведенному алгоритму, следует вычесть 1.

Пример

Рассмотрим дерево, приведенное в примере. Рядом с каждой вершиной указан размер поддерева, если рассматривать эту вершину в качестве корня. Вершины 1, 3 и 6 имеют поддеревья с четным количеством вершин. Поскольку вершина 1 является корнем и не имеет ребра, ведущего к предку, мы удаляем два ребра: (1, 3) и (1, 6).

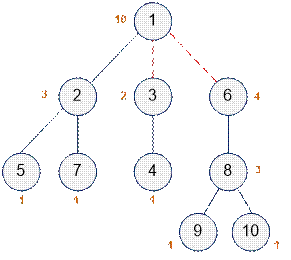
Дерево распалось на 3 компоненты связности, каждая из которых содержит четное количество вершин.

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 101

int g[MAX][MAX], used[MAX];

Функция dfs совершает поиск в глубину из вершины v и возвращает количество вершин в поддереве с корнем v.

int dfs(int v)

{

used[v] = 1;

В переменной s вычисляем количество вершин в поддереве с корнем v.

int s = 1;

Перебираем сыновей i вершины v. Прибавляем к s значения dfs(i).

for (int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) s += dfs(i);

Если размер поддерева s четный, удаляем ребро между v и его предком.

if (s % 2 == 0) res++;

Возвращаем количество вершин в поддереве с корнем v.

return s;

}

Основная часть программы. Читаем входные данные. Строим граф.

scanf("%d %d", &n, &m);

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = g[b][a] = 1;

}

Запускаем поиск в глубину из вершины 1. В переменной res подсчитываем количество удаленных ребер.

res = 0;

dfs(1);

Ребра из 1 в его предка не существует. Выводим res – 1.

printf("%d\n", res - 1);

Python реализация

Функция dfs совершает поиск в глубину из вершины v и возвращает количество вершин в поддереве с корнем v.

def dfs(v):

used[v] = 1

В переменной s вычисляем количество вершин в поддереве с корнем v.

s = 1

Перебираем сыновей i вершины v. Прибавляем к s значения dfs(i).

for i in range(1, n + 1):

if g[v][i] and not used[i]:

s += dfs(i)

Если размер поддерева s четный, удаляем ребро между v и его предком.

if s % 2 == 0:

global res

res += 1

Возвращаем количество вершин в поддереве с корнем v.

return s

Основная часть программы. Читаем входные данные. Строим граф.

n, m = map(int, input().split())

g = [[0] * (n + 1) for _ in range(n + 1)]

used = [0] * (n + 1)

for _ in range(m):

a, b = map(int, input().split())

g[a][b] = g[b][a] = 1

Запускаем поиск в глубину из вершины 1. В переменной res подсчитываем количество удаленных ребер.

res = 0

dfs(1)

Ребра из 1 в его предка не существует. Выводим res – 1.

print(res - 1)